How to Determine if a Vector Field Is Conservative

Calculus III
© The scientific sentence. 2010
Calculus III:
Conservative vector fields
Let's recall that if a vector field  is conservative then ∫C
is conservative then ∫C  .
. 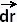 is independent of path.
is independent of path.
This comes from that if the vector field  is conservative then it is associated to a potential function f such as ∇f =
is conservative then it is associated to a potential function f such as ∇f =  , and, in turn, using the fondamental theorem of line integrals.
, and, in turn, using the fondamental theorem of line integrals.
Now, given a vector field  , we want to:
, we want to:
• determine whether  is conservative, and
is conservative, and
• If so, determine its potential function f.
1. Given  . Is it conservative ?
. Is it conservative ?
Given a vector field, we want to identify if it is conservative.
The vector field  is conservative. It is then associated to a potential function f such as ∇f =
is conservative. It is then associated to a potential function f such as ∇f = 
 = P
= P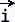 + Q
+ Q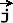 = (∂f/∂x)
= (∂f/∂x)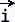 + (∂f/∂y)
+ (∂f/∂y)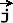 . So
. So
∂f/∂x = P
∂f/∂y = Q
Taking the partial derivative, we obtain:
∂2f/∂x∂y = ∂P/∂y
∂2f/∂y∂x = ∂Q/∂x
Therefore
∂P/∂y = ∂Q/∂x
Theorem:
Let  = P
= P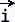 + Q
+ Q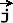 be a vector field on an open and simply-connected region D.
be a vector field on an open and simply-connected region D.
If P and Q have continuous first order partial derivatives in D and ∂P/∂y = ∂Q/∂x,
then the vector field  is conservative.
is conservative.
Example 1
Determine if the vector fields
 (x,y) = (x2 + y)
(x,y) = (x2 + y)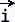 + (y2 + x)
+ (y2 + x)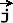
is conservative or not.
We have:
P(x,y) = x2 + y
Q(x,y) = y2 + x
∂P/∂y = 1
∂Q/∂x = 1
∂P/∂y = ∂Q/∂x
 (x,y) is conservative.
(x,y) is conservative.
Example 2
Determine if the vector fields
 (x,y) = (x2 + xy)
(x,y) = (x2 + xy)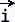 + (y2 + xy)
+ (y2 + xy)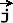
is conservative or not.
We have:
P(x,y) = x2 + xy
Q(x,y) = y2 + xy
∂P/∂y = x
∂Q/∂x = y
∂P/∂y ≠ ∂Q/∂x
 (x,y) is not conservative.
(x,y) is not conservative.
2.  is conservative.
is conservative.
What is its potential function ƒ ?
Given a conservative vector field, we want to determine the potential function ƒ for this vector field.
Let�s assume that the vector field  is conservative and so we know that a potential function, f(x,y) exists. We can then write:
is conservative and so we know that a potential function, f(x,y) exists. We can then write:
∇f = (∂f/∂x)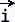 + (∂f/∂y)
+ (∂f/∂y)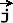 = P
= P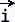 + Q
+ Q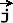 =
=  .
.
That is, by setting the two components equal:
∂f/∂x = P, and
∂f/∂y = Q
By integrating each of these, we obtain the two following equations.
f(x,y) = ∫P(x,y) dx or f(x,y) = ∫Q(x,y) dy
Example 3
Determine if the vector field
 = (x2y3 + x)
= (x2y3 + x)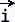 + (x3y2 + y)
+ (x3y2 + y)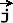
is conservative and if so, find a potential function for this vector field.
We have:
P(x,y) = x2y3 + x
Q(x,y) = x3y2 + y
∂P/∂y = 3 x2y2
∂Q/∂x = 3 x2y2
∂P/∂y = ∂Q/∂x
So  (x,y) is conservative.
(x,y) is conservative.
Now let�s find the potential function:
f(x,y) = ∫P(x,y) dx = ∫ (x2y3 + x) dx = c(y) is the a function of y.
(1/3)x3y3 + (1/2) x2 + c(y)
This function is constant with respect to x.
f(x,y) = ∫Q(x,y) dy = ∫ (x3y2 + y) dy = c(x) is a function of x.
(1/3)x3y3 + (1/2) y2 + c(x)
This function is constant with respect to y.
Let's work on the first integral:
f(x,y) = (1/3)x3y3 + (1/2) x2 + c(y)
We now need to determine c(y) .
Let�s differentiate f(x,y) with respect to y and set it equal to Q:
∂f/∂y = x3y2 + ∂c(y)/∂y = Q = x3y2 + y.
Hence ∂c(y)/∂y = y , and then
c(y) = (1/2) y2 + const.
Threrfore
f(x,y) = (1/3)x3y3 + (1/2) x2 + (1/2) y2 + const.
The constant const can be anything. So there are an infinite number of possible potential functions, although they will differ by an additive constant.
3. Three-dimentional conservative vector fields
Example 4
Find the potential function for the vector field
 (x,y,z) = 2xy2z3
(x,y,z) = 2xy2z3 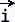 + 2x2yz3
+ 2x2yz3 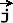 + 3x2y2z2
+ 3x2y2z2 
We will see in the second next section that the curl of this vector field  (x,y,z) in zero. So this vector field is conservative.
(x,y,z) in zero. So this vector field is conservative.
Now, we have:
P(x,y,z) = ∂f/∂x = 2xy2z3
Q(x,y,z) = ∂f/∂y = 2x2yz3
R(x,y,z) = ∂f/∂z = 3x2y2z2
Let�s find the potential function:
Let's integrate the first one with respect to x :
f(x,y,z) = x2y2z3 + c(y,z)
• Now, we differentiate this with respect to y and set it equal to Q:
2x2yz3 + ∂c(y,z)/∂y = 2x2yz3
Hence ∂c(y,z)/∂y = 0. That is c(y,z) = c(z)
Therefore
f(x,y,z) = x2y2z3 + c(z)
• Now, we differentiate with respect to z and set the result equal to R:
3x2y2z2 + ∂c(z)/∂z = 3x2y2z2
Hence ∂c(z)/∂z = 0. That is c(z) = const.
The potential function for this vector field is then:
f(x,y,z) = x2y2z3 + const.
How to Determine if a Vector Field Is Conservative
Source: https://scientificsentence.net/Equations/CalculusIII/index.php?key=yes&Integer=conservative_vector_fields